I’m a pretty big fan of pencil-and-paper logic puzzles, the kind which can be solved by deduction and which tend to reduce to the exact cover problem. Some of these puzzles have entered the mainstream, such as Sudoku and Kakuro of Dell Mag and Nikoli fame.

There are a great number of puzzles beyond those two, and here I’ll cover some of the less well-known ones that I like. This page is perpetually under construction.

Gokigen Naname (ごきげん ななめ), or Slant, is a Nikoli puzzle where you fill in all the squares of a grid with diagonal lines. Numbers specified at certain intersections denote how many diagonals touch that intersection. Diagonals may not form closed loops. While relatively simple as a concept, it’s a really fun puzzle to solve because there are a number of interesting deduction strategies.

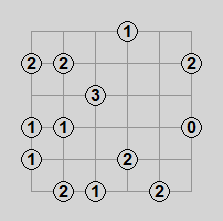
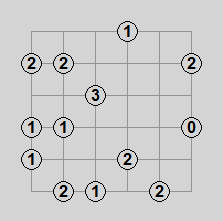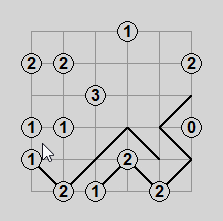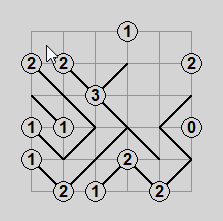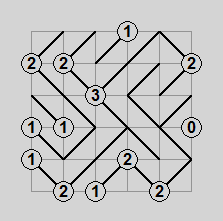
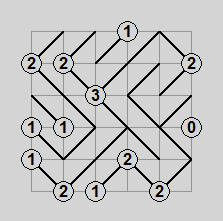
unsolved puzzle   animated solution   solved puzzle

Pictured above are a simple Slant puzzle, an animated solution, and the solved state.

Slant is not very well known occidentally, but Simon Tatham’s puzzle collection can generate Slant puzzles of varying size and difficulty.

The Kjarposko—named for its inventor, Kjartan Poskitt, of the Murderous Maths series of children’s math books—features N dominos joined by lines. The task is to place the numbers from 1 to N in the bottoms of the dominos, so that the top of every domino shows the sum of the bottoms of the dominos that are linked to it.

They are odd but quite addicting puzzles. Kjarposkos were introduced in the MM book Kakuro and Other Fiendish Number Puzzles, which features 21 of them, plus two small practice puzzles. The MM website also features 31 daily Kjarposkos, reusing 20 of the puzzles from the book alongside 11 new ones. Which puts the total number of published Kjarposko puzzles at 34.

As of 2019, the Murderous Maths Twitter account has been posting simplified versions of Kjarposkos in a regular series called K-PUZZ. They are smaller and meant to take less than 5 minutes to solve.